The field \(\mathbb{F}_p\) with \(p\) elements has a finite extension of degree \(n\) for each natural number \(n\). On Twitter, @syzygay1 asked if this can be extended to infinite field extensions of \(\mathbb{F}_p\) for a generalized notion of “degree”. For the field \(\mathbb{F}_p\), this leads to the concept of supernatural numbers, which are connected to the Arithmetic Site of Connes and Consani. It is interesting to see what happens for other fields as well, and this is what led me to write the notes below.
After looking at the case of the field \(\mathbb{F}_p\), we discuss the Pontryagin dual of the absolute Galois group, what this has to do with the field with one element, and how we could classify algebraic extensions for fields other than \(\mathbb{F}_p\).
Supernatural numbers
The problem was first studied by Ernst Steinitz in his 1910 paper “Algebraische Theorie der Körper” (“Algebraic Theory of Fields”). He showed that the algebraic extensions of \(\mathbb{F}_p\) correspond to what are now called the supernatural numbers or Steinitz numbers. The idea behind it was rediscovered by @syzygay1 on Twitter. Each algebraic extension \(K/\mathbb{F}_p\) is the union of its finite subfields, so we have to keep tracks of which finite subfields occur. If \(K\) contains \(\mathbb{F}_{p^n}\), the (unique) field extension of \(\mathbb{F}_p\) that has degree \(n\), then \(K\) also has to contain all subfields of \(\mathbb{F}_{p^n}\). These are precisely the fields \(\mathbb{F}_{p^m}\) for \(m\) a divisor of \(n\). Further, if \(K\) contains two fields \(\mathbb{F}_{p^k}\) and \(\mathbb{F}_{p^r}\) of degree \(k\) and \(r\), then it also contains the union of these two fields, which is \(\mathbb{F}_{p^l}\) for \(l\) the least common multiple of \(k\) and \(r\).

There is an analogy with divisors here. If a natural number \(s\) is divisible by \(n\), then it is also divisible by each \(m\) as long as \(m\) divides \(n\). And if \(s\) is divisible by \(k\) and \(r\), then it is also divisible by the least common multiple of \(k\) and \(r\).
So we can define a supernatural number as a subset \(S \subseteq \{1,2,3,\dots\}\) such that:
- if \(n\in S\) and \(m\) divides \(n\) then \(m \in S\);
- if \(k, r \in S\) then the least common multiple of \(k\) and \(r\) is also in \(S\).
Then each supernatural number \(S\) defines a field extension \(\bigcup_{n \in S} \mathbb{F}_{p^n}\) and every algebraic extension is of this form.
One problem: with this definition supernatural numbers don’t look like numbers. The remedy is that you can think of each supernatural number \(S \subseteq \{1,2,3,\dots \}\) as the set of divisors of a formal product \(\prod_p p^{n_p}\), where the product is over all primes, and each exponent \(n_p\) is in \(\{0,1,2,3,\dots\}\cup\{\infty\}\). This is how supernatural numbers are usually defined.
Similar base fields
Steinitz managed to give a very precise classification of the algebraic extensions of the finite field \(\mathbb{F}_p\). Can we do something similar for other base fields?
The only property of \(\mathbb{F}_p\) that was used is that \(\mathbb{F}_p\) has a unique extension of degree \(n\) for each natural number \(n\), and that the extension of degree \(m\) is contained in the extension of degree \(n\) if and only if \(m\) divides \(n\).
This property holds for other fields as well, for example for any finite field (with cardinality a prime power and not necessarily a prime).
We can also use Steinitz’s classification to find an infinite field with this property. Take for example \(S\) the set of squarefree natural numbers. This corresponds to the formal product \(s=\prod_p p\) over all primes \(p\). In this case, there is also a unique extension of degree \(n\), namely the one corresponding to the product \(n\cdot s\). So for this field, the algebraic extensions are again classified by the supernatural numbers.
We also don’t have to restrict ourselves to field extensions. If \(\mathrm{M}_n(\mathbb{C})\) is the ring of \(n\times n\) matrices over the complex numbers, then there is a ring morphism \(\mathrm{M}_m(\mathbb{C}) \to \mathrm{M}_n(\mathbb{C})\) if and only if \(m\) divides \(n\). This is exactly the same situation as with field extensions… So for a supernatural number \(s\) we can look at the union of a sequence \(\mathrm{M}_{n_1}(\mathbb{C}) \subseteq \mathrm{M}_{n_2}(\mathbb{C}) \subseteq \dots\) where \(n_1, n_2,\dots\) are divisors of \(s\), each one dividing the next one, such that \(n_i\) “converges” to \(s\). Modulo some analysis, these infinite unions are precisely the UHF-algebras. So UHF-algebras can also be classified using supernatural numbers.
Visualizing the supernatural numbers
All this is a good excuse for me to bring up the visualizations that I made of the supernatural numbers, see the previous post. Here is one of them:
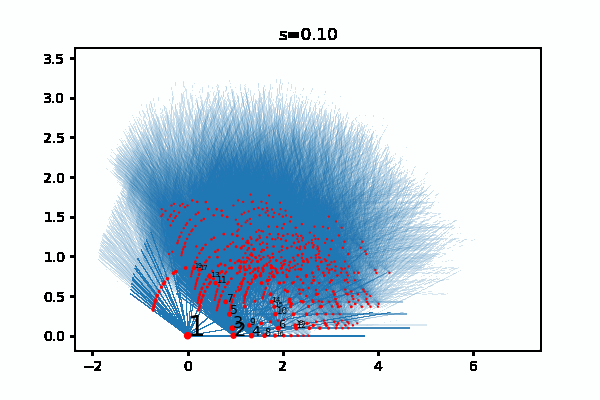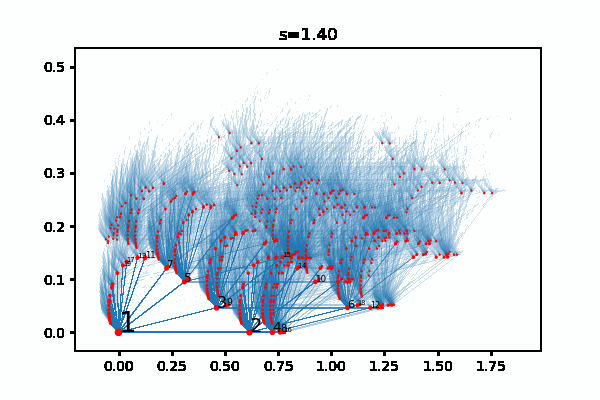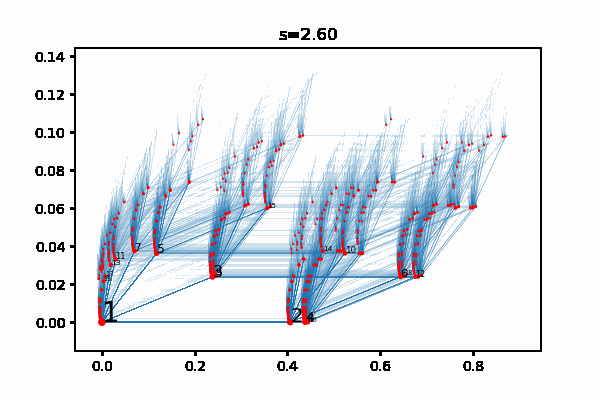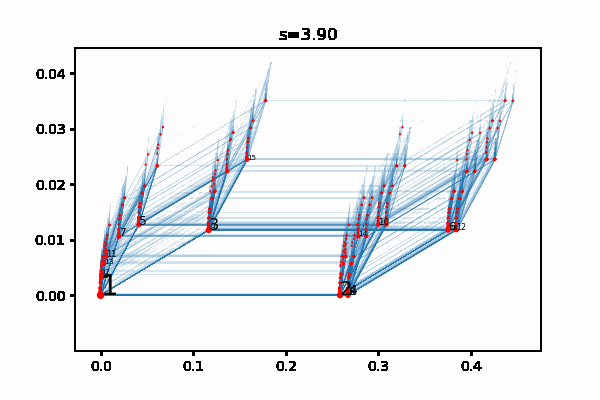
The red dots represent finite extensions, and they converge in \(\mathbb{R}^2\) to supernatural numbers that represent algebraic extensions.
Relation to the Galois group
Algebraic extensions correspond to closed subgroups of the absolute Galois group, according to the fundamental theorem of Galois theory. For \(\mathbb{F}_p\), the absolute Galois group is isomorphic to the additive group of profinite integers \(\hat{\mathbb{Z}}\). The closed subgroups of finite index are the subgroups \(n\hat{\mathbb{Z}} \subseteq \hat{\mathbb{Z}}\) for \(n\) a natural number. The more general subgroups can be written as an intersection of closed subgroups of finite index.
To determine the closed subgroups, you can also use Pontryagin duality. There is a bijective correspondence between closed subgroups of an abelian topological group \(G\), and closed subgroups of the Pontryagin dual group \(G^*\), see here.
In the case of the field \(\mathbb{F}_p\), the absolute Galois group is \(\hat{\mathbb{Z}}\) and this has as Pontryagin dual \(\mathbb{Q}/\mathbb{Z}\), with the discrete topology. (Galois groups are compact so they always have a discrete group as Pontryagin dual.) So algebraic extensions of \(\mathbb{F}_p\) correspond to subgroups of \(\mathbb{Q}/\mathbb{Z}\), or in other words, subgroups of \(\mathbb{Q}\) that contain \(\mathbb{Z}\).
It follows that the subgroups of \(\mathbb{Q}\) that contain \(\mathbb{Z}\) are also classified by the supernatural numbers. The subgroup corresponding to the supernatural number \(s\) contains precisely the fractions such that (in reduced form) the denominator is a divisor of \(s\).
The field with one element
To get a bit of intuition for Pontryagin duality, it is good to take a look at the (conjectural) field with one element \(\mathbb{F}_1\). There is no fixed definition of what \(\mathbb{F}_1\) is exactly, but there are a lot of properties that it should satisfy. For example, since the absolute Galois group of \(\mathbb{F}_p\) is isomorphic to \(\hat{\mathbb{Z}}\) for all primes \(p\), we can say that, by analogy, the absolute Galois group of \(\mathbb{F}_1\) is also isomorphic to \(\hat{\mathbb{Z}}\). This means in particular that \(\mathbb{F}_1\) has a unique extension of degree \(n\) for each natural number \(n\).
One definition of \(\mathbb{F}_1\) is that \(\mathbb{F}_1\) is the trivial monoid, and that ring extensions of \(\mathbb{F}_1\) are arbitrary commutative monoids. The idea is that we forget addition and only look at multiplication. The multiplicative group of a finite field is cyclic, so the finite field extensions of \(\mathbb{F}_1\) should be the finite cyclic groups. Fortunately, there is a unique cyclic group of order \(n\) for each natural number \(n\), so the field extensions are how we want them.
Pontryagin duality shows up here in an interesting way: the algebraic closure of \(\mathbb{F}_1\), in the above definition, is the group \(\mathbb{Q}/\mathbb{Z}\), which is precisely the Pontryagin dual of the absolute Galois group.
More general base fields
Can we classify the algebraic extensions of a general field \(K\), similarly to how we classified the algebraic extensions of \(\mathbb{F}_p\)? The answer is probably no, because Galois theory is too difficult for general fields. A first obstruction is that in general the absolute Galois group is not abelian. So we cannot use Pontryagin duality, and as an alternative we probably have to look at \(n\)-dimensional representations of the Galois group, and these are very complicated.
So we’ll have a look at two examples with abelian Galois group.
The first example that springs to mind is to look at the abelian extensions of \(\mathbb{Q}\). These are the Galois extensions of \(\mathbb{Q}\) that have abelian Galois group. Alternatively, these are the extensions of \(\mathbb{Q}\) that are contained in the maximal abelian extension \(\mathbb{Q}^\mathrm{ab}\). By the fundamental theorem of Galois theory, we now know that the abelian extensions of \(\mathbb{Q}\) correspond to the closed subgroups of the Galois group \(\mathrm{Gal}(\mathbb{Q}^\mathrm{ab}/\mathbb{Q})\).
This Galois group can be computed using Kronecker-Weber theorem: up to isomorphism you get \(\hat{\mathbb{Z}} \times \prod_n \mathbb{Z}/n\mathbb{Z}\), where the product is over all integers \(n\) (see e.g. Lenstra’s notes on profinite groups). For the Pontryagin dual we then find \(\mathbb{Q}/\mathbb{Z} \times \bigoplus_n \mathbb{Z}/n\mathbb{Z}\). So abelian extensions of \(\mathbb{Q}\) correspond to subgroups of \(\mathbb{Q}/\mathbb{Z} \times \bigoplus_n \mathbb{Z}/n\mathbb{Z}\) . At the moment, I have no idea how to describe the subgroups of a group like this in a nice way. It is already difficult to describe the subgroups of \(G \times H\) if you know the subgroups of \(G\) and the subgroups of \(H\), see the explanation here. For infinite products or infinite direct sums this seems impossible. The difficulty does not appear for \(\hat{\mathbb{Z}}=\prod_p \mathbb{Z}_p\) because the orders of finite quotients of \(\mathbb{Z}_p\) are coprime to the orders of finite quotients of \(\mathbb{Z}_q\), for \(p \neq q\).
We can simplify the situation a lot by looking at the field \(\mathbb{Q}(\sqrt{\mathbb{Q}})\). This is the notation I borrowed from Hendrik Lenstra’s book on Galois theory for schemes. As the notation suggests, it is the extension of \(\mathbb{Q}\) that you get by adjoining all elements \(\sqrt{a}\) for \(a \in \mathbb{Q}\). The Galois group of \(\mathbb{Q}(\sqrt{\mathbb{Q}})\) over \(\mathbb{Q}\) is isomorphic to \(\prod_{i \in I} \mathbb{Z}/2\mathbb{Z}\) for some countably infinite set \(I\) (this is Exercise 2.14 of Lenstra’s book). So the Pontryagin dual is \(\bigoplus_{i \in I} \mathbb{Z}/2\mathbb{Z}\). Its subgroups are complicated, but not extremely complicated. We can interpret \(\bigoplus_{i \in I} \mathbb{Z}/2\mathbb{Z}\) as a vector space of countably infinite dimension over \(\mathbb{F}_2\), and then the subgroups are precisely the vector subspaces.
I would be interested in a classification of certain algebraic extensions of \(\mathbb{C}(t)\) as well. The absolute Galois group of \(\mathbb{C}(t)\) is the profinite completion of the free group with \(\kappa\) many generators, where \(\kappa\) is the cardinality of the complex numbers. The Pontryagin dual is then the product \(\prod_J \mathbb{Q}/\mathbb{Z}\) over an index set \(J\) of cardinality \(\kappa\). So the abelian extensions of \(\mathbb{C}(t)\) should correspond to the subgroups of \(\prod_J \mathbb{Q}/\mathbb{Z}\). This does not seem like a very useful description. Maybe we can simplify the situation by allowing only abelian extensions that are ramified at a prescribed set of points. But I don’t really understand how this works… let me know if you have some ideas!
