This is a follow-up post of the one yesterday about the fundamental group of a monoid. There we looked at the covering spaces of the free monoid on two generators, and covering spaces of categories in general. From there it is a small(ish) step towards defining covering spaces of toposes, which in turn can be used to make sense of what the fundamental group of a topos should be.
The idea is that toposes are a common “playground” for many geometrical concepts. In order to study a scheme we can look at its étale topos, or to study a topological space we can look at the topos of local homeomorphisms to it. Defining a fundamental group for general toposes means that you can talk about fundamental groups in very different settings, and you can start comparing situations that were otherwise completely foreign to each other (I try to give a concrete example at the end).
Covering spaces of a topos
A topos is a category satisfying some technical axioms. Fortunately, you don’t need these axioms in order to do computations with toposes, for example if you want to compute the fundamental group of a topos.
Every topos has a terminal object \(1\) which means that for every object \(E\) in the topos there is a unique morphism \(E \to 1\). The idea is that \(1\) is the “base space” and each morphism \(E \to 1\) can be interpreted as a local homeomorphism to the base space. For example, if \(X\) is a topological space, then the local homeomorphisms \(Y \to X\) form a topos, and the terminal object is the trivial local homeomorphism \(X \to X\) (the “base space”).

What is a covering space of a topos? Can we just pretend it is an ordinary category and compute the covering spaces in this sense?
This doesn’t work: if a category \(\mathcal{C}\) has a terminal object, then its fundamental groupoid is equivalent to the trivial group. So all discrete fibrations are of the form \(\mathcal{D} \to \mathcal{C}\) where \(\mathcal{D}\) is the disjoint union of some copies of \(\mathcal{C}\).
To get a meaningful notion of fundamental group for a topos, we need to take into account the “canonical Grothendieck topology” on the topos, as follows. We say that a family of morphisms \(\{f_i: E_i \to E\}_{i \in I}\) covers the target \(E\) if and only if \(\bigcup_{i \in I} f_i(E_i)=E\). The axioms for toposes make sure that this expression makes sense.
The definition of a covering space of a topos \(\mathcal{E}\) is now as follows. It is a discrete fibration \(\pi : \mathcal{E'} \to \mathcal{E}\) which is a covering space of categories locally. More precisely, we need that there is a full subcategory \(\mathcal{U} \subseteq \mathcal{E}\) such that:
- all objects in \(\mathcal{E}\) can be covered by objects in \(\mathcal{U}\), and
- each \(f : X \to X'\) in \(\mathcal{U}\) and object \(Y'\) in \(\mathcal{E}'\) with \(\pi(Y') = X'\), there is a unique \(\tilde{f} : Y'' \to Y'\) with \(\pi(\tilde{f}) = f\).
In fact, if \(\mathcal{U} \subseteq \mathcal{E}\) is a full subcategory such that every object of \(\mathcal{E}\) is covered by the objects in \(\mathcal{U}\), then any covering space of categories \(\mathcal{U}' \to \mathcal{U}\) extends to a covering space of toposes \(\mathcal{E}' \to \mathcal{E}\).
Why is the above the right definition for a covering space of a topos? One reason is that it extends the definition of covering space for topological spaces. For a connected, locally connected topological space \(X\), we can look at the topos \(\mathcal{E}\) consisting of the local homeomorphisms \(Y \to X\) with fixed target \(X\). In this case, the covering spaces of the topos are all of the form \(\mathcal{E'} \to \mathcal{E}\) where \(\mathcal{E}'\) is the topos associated to a covering space \(Y\) of \(X\).
Fundamental group of a topos
After defining covering spaces for toposes \(\mathcal{E}\), it remains to find a group \(G\) such that covering spaces of \(\mathcal{E}\) correspond precisely to sets with a \(G\)-action. This can go wrong in various ways.
The problem already appears for topological spaces. Take for example the shrinking wedge of circles:
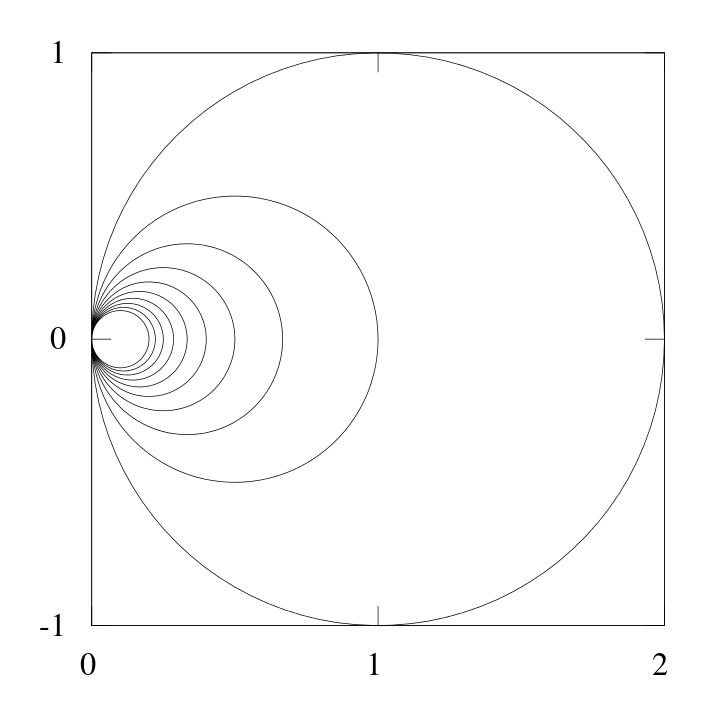
Suppose that you have a family of covering space \(Y_i \to X\) with as base space \(X\) the shrinking wedge of circles. Then the disjoint union \(\bigsqcup_{i \in I} Y_i \to X\) is not necessarily a covering space anymore. The reason is that, while for each covering space you can find an open cover \(X = \bigcup_{j \in J} U_j\) that trivializes \(Y_i\), it is not possible to find a common open covering that works for all covering spaces at once.
This is in contrast to what happens what happens for sets with a \(G\)-action, for \(G\) a group: for any family of sets \(S_i\), each equipped with a \(G\)-action, the disjoint union \(\bigsqcup_{i \in I} S_i\) is still a set with a \(G\)-action.
So something has to go wrong in the correspondence between covering spaces of \(X\) and sets with a \(G\)-action, regardless of what group \(G\) you pick.
One possible solution is to settle for less, and try to find a group \(G\) such that at least the “connected” covering spaces of the topos \(\mathcal{E}\) are the same as sets with a transitive \(G\)-action.
Even this is not always possible. For example, if \(\mathcal{E}\) is the small étale topos associated to the field of rational numbers \(\mathbb{Q}\) then connected covering spaces \(\mathcal{E}' \to \mathcal{E}\) correspond to finite field extensions of \(\mathbb{Q}\). And there is no (discrete) group \(G\) such that the finite field extensions of \(\mathbb{Q}\) correspond to the sets with transitive \(G\)-action.
But in this case there is a profinite group \(G\) such that sets with a continuous, transitive \(G\)-action correspond to finite field extensions of \(\mathbb{Q}\), namely the absolute Galois group \(G=\mathrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})\).
For an arbitrary connected, locally connected topos, you can similarly construct a pro-group that functions as a fundamental group. Pro-groups are very technical, but it is the best that can be done at this level of generality. Moerdijk in “Prodiscrete groups and Galois toposes” shows that pro-groups can be seen as a special kind of localic group, similar to how profinite groups are a special kind of topological group.
Questions
Every connected, locally connected topos has a fundamental group. Sometimes it is a discrete group, sometimes it is a profinite group or even a pro-group. We can now start wondering about whether two completely different toposes can have the same fundamental group. For example, if \(M\) is the free monoid on two generators, then the topos of sets with an \(M\)-action has the same fundamental group as the topos of local homeomorphisms to the figure eight space.
Here are some questions that I think are interesting:
- If \(\mathcal{E}\) is the topos of local homeomorphisms to a topological space \(X\), then how does the fundamental group of \(\mathcal{E}\) relate to the fundamental group of \(X\) (defined in terms of paths in \(X\))?
- For a given profinite group \(G\), let’s say \(G = \mathrm{Gal}(\bar{\mathbb{Q}}/\mathbb{Q})\), can we find a topological space \(X\) such that the topos associated to \(X\) has \(G\) as fundamental group? Here \(X\) should be a pathological topological space like the shrinking wedge of circles, as otherwise the fundamental group of the topos is discrete.
