I’m still trying to improve my understanding of algebraic extensions of \(\mathbb{C}(t)\). It’s a problem that’s connected to a lot of interesting mathematical ideas, like Riemann surfaces, the étale fundamental group, dessins d’enfants and modular curves.
The connection to Riemann surfaces is as follows: algebraic extensions of \(\mathbb{C}(t)\) correspond to maps \(\pi:\Sigma \to \mathbb{P}_\mathbb{C}^1\) where \(\Sigma\) is a Riemann surface, \(\mathbb{P}^1_\mathbb{C}\) is the complex projective line, and \(\pi\) is a local homeomorphism except in a few so-called ramifications points \(x_1,\dots,x_r \in \Sigma\).
What is a Riemann surface?
A big “bottleneck” in my understanding was that I didn’t really know the definition of a Riemann surface. I would have guessed that it was an oriented Riemannian manifold of dimension 2 or maybe a Kähler manifold of real dimension 2. It turns out that these two definitions are equivalent (see Remark 4 here). But both are wrong.
The actual definition: a Riemann surface is a 1-dimensional complex manifold. You can always construct a Riemannian metric that is compatible with the complex structure, but this Riemannian metric is only unique up to conformal equivalence. This means that for two such metrics \(g\) and \(g'\) there is a positive real function \(\lambda\) such that \(g' = \lambda g\). The underlying reason is that, locally, holomorphic maps are precisely the smooth maps that are angle-preserving and orientation-preserving. You can look up the details here.
Every oriented Riemannian 2-manifold has an underlying Riemann surface (by considering the metric up to conformal equivalence). This is because, as mentioned above, a 2-manifold like this can always be made into Kähler manifold, in a unique way. In other words, there is automatically a complex manifold structure on it that is compatible with the metric. This is a bit crazy, and it certainly doesn’t happen for oriented Riemanian manifolds in higher dimensions…
As an example, take the donut:

By “donut” I mean a torus that is curved like a real donut, so it is equipped with the Riemannian metric that it inherits from the embedding in \(\mathbb{R}^3\). You can turn this donut into a complex manifold such that the complex structure and the Riemannian metric are compatible. This is new to me, because I thought only flat tori (quotients of \(\mathbb{C}\) by a lattice) could be equipped with a compatible structure of complex manifold.
Elliptic, parabolic, hyperbolic
The metric on a Riemann surface is only determined up to conformal equivalence. However, some metrics are considered to be ‘better’ than others, and this changes the way geometers talk about Riemann surfaces. For example, some people might say that donuts are flat (zero curvature), and as you can see on the picture this is not necessarily true. What is meant is that on a donut every Riemannian metric is conformally equivalent to a flat metric, and this flat metric is considered to be the metric that you should look at.
Another example is a complex plane with some points removed. The complex plane with the Euclidean metric is flat, and after removing a few points, the restriction of this metric is still flat. However, this is not the metric. The metric that complex geometers see, after removing at least two points, is an hyperbolic metric (conformally equivalent to the flat one).
The hyperbolic metric that you get is complete, and the removed points are called cusps or cusp singularities (not to be confused with cusps in algebraic geometry).
The kind of metric that is preferred depends on the universal cover of the Riemann surface. The universal cover is again a complex surface and the covering map is a local isomorphism (or local biholomorphism in complex analysis terminology). It turns out that there are only three possibilities for the universal cover:
- The complex projective line \(\mathbb{P}_\mathbb{C}^1\) (the parabolic case).
- The complex plane \(\mathbb{C}\) (the elliptic case).
- The unit disk \(D(0,1) = \{ z \in \mathbb{C} : \lvert z \rvert < 1 \}\) (the hyperbolic case).
In order to make these three into Riemann surfaces, you need to specify the structure of complex manifold in each case. For \(\mathbb{P}_\mathbb{C}^1\) this is the usual construction, for \(\mathbb{C}\) this is trivial, and \(D(0,1)\) inherits the one from \(\mathbb{C}\) by being an open subset of it.
For each of these three Riemann surfaces, there is a “favorite” metric that is compatible with the complex structure.
- On \(\mathbb{P}^1_\mathbb{C}\) you can construct a metric with constant curvature, called the Fubini—Study metric. The complex projective line is homeomorphic to a sphere, and the Fubini—Study metric is the usual metric you get from the embedding of the sphere in \(\mathbb{R}^3\). The constant curvature is positive, so after rescaling you can assume it to be \(1\).
- The complex plane \(\mathbb{C}\) is an open subset of \(\mathbb{P}^1_\mathbb{C}\) but the restriction of the Fubini—Study metric is no longer complete. However, the Euclidean metric is complete. It is also of constant curvature, this time of constant curvature \(0\).
- The unit disk \(D(0,1)\) is an open subset of \(\mathbb{C}\) but the restriction of the Euclidean measure is no longer complete (and neither is the restriction of the Fubini—Study metric). However, there is another metric, the Poincaré metric, which is complete and has constant curvature. The constant curvature is negative, so after rescaling you can assume it to be \(-1\).

If you have a Riemann surface \(\Sigma\), you can look at the universal cover \(\widetilde{\Sigma}\), and put the corresponding “favorite” metric on it. Now something weird happens… this metric always descends to a metric on \(\Sigma\).
The reason why is explained well here, but I’ll repeat the argument. You can write \(\Sigma\) as the quotient \(\widetilde{\Sigma}/\Gamma\) where the discrete group \(\Gamma\) has a holomorphic group action on \(\widetilde{\Sigma}\) that is free and properly discontinuous. In order for the metric on \(\widetilde{\Sigma}\) to descend to a metric on \(\Sigma\), we need that the group \(\Gamma\) acts by isometries. So the action of \(\Gamma\) should not only preserve angles but also areas. Let us look at why this is the case in the three cases:
- On \(\mathbb{P}^1_\mathbb{C}\) the holomorphic self-maps are maps \(z \mapsto \frac{az+b}{cz+d}\) with \(\begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \mathrm{PGL}_2(\mathbb{C})\). These all have a fixpoint, so there are no free holomorphic group actions on \(\mathbb{P}^1_\mathbb{C}\). The only Riemann surface with \(\mathbb{P}^1_\mathbb{C}\) as universal cover is \(\mathbb{P}^1_\mathbb{C}\) itself.
- On \(\mathbb{C}\) the holomorphic self-maps are the same maps \(z \mapsto \frac{az+b}{cz+d}\) but now they have to fix the point at infinity. By l’Hôpital’s rule this means that \(\tfrac{a}{c}=\infty\) or in other words \(a \neq 0\) and \(c = 0\). So the holomorphic self-maps are of the form \(z \mapsto az + b\) for \(a,b \in \mathbb{C}\). If there are no fixpoints, then necessarily \(a = 1\), otherwise there is a solution to \(z = az+b\). So the holomorphic self-maps without fixpoints are the translations, and these are all isometries.
- For the unit disk \(D(0,1)\) every holomorphic self-map is an isometry, see Theorem 1.5 of Bowman’s lectures notes on hyperbolic geometry.
So the special metrics on the universal cover \(\widetilde{\Sigma}\) always descend to a metric on the original Riemann surface \(\Sigma\), so that the covering map is a local isometry. This implies that the metric on \(\Sigma\) is again complete and of constant curvature \(-1\), \(0\) or \(1\).
A complete metric of constant curvature on \(\Sigma\) lifts to a complete metric of constant curvature on \(\widetilde{\Sigma}\). This can only be the special metric described above. So on each Riemann surface, there is a unique complete metric of constant curvature, up to scaling.
Ricci flow
In 2003, Grigori Perelman proved the Poincaré Conjecture. Essential to his work was the so-called Ricci flow: a Riemannian metric \(g_{ij}(t)\) on a fixed manifold varying in function of a time parameter \(t\) such that a certain differential equation is satisfied. When awarded the Clay Millenium Prize, Perelman claimed that his contribution was no greater than that of Richard Hamilton, who introduced the Ricci flow.
For compact Riemann surfaces, the Ricci flow is extremely well-behaved. If you choose an initial Riemannian metric, compatible with the complex structure, then throughout the Ricci flow the Riemannian metric \(g_{ij}(t)\) is still compatible with the complex structure, i.e. conformally equivalent to the initial one.
Further, the Ricci flow converges to a metric of constant curvature. This was proved by Hamilton in 1988 (in “The Ricci flow on surfaces”), except in the case of a sphere that has regions where the curvature is negative, as in the picture below.
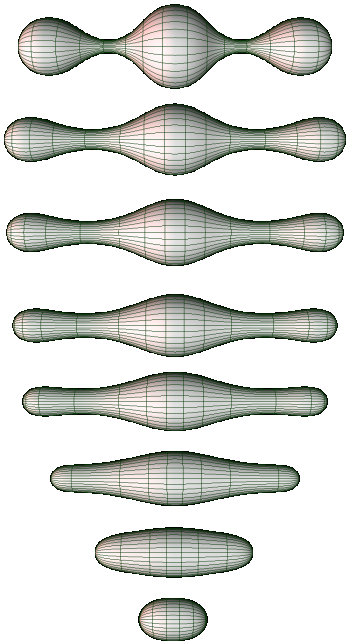
Bennett Chow (in “The Ricci flow on the 2-sphere”) later showed that for any initial metric on the sphere, the curvature becomes positive at each point, after some time in the Ricci flow. This is as illustrated above: at first there are regions of negative curvature but they are gone in the last two stages. And then it starts converging to a constant curvature metric because of Hamilton’s results.
For surfaces that are not compact, the research is more recent. Giesen and Topping showed that, for general hyperbolic Riemann surfaces, the Ricci flow exists and converges locally to the complete hyperbolic metric of constant curvature. The caveat is that at certain points in the Ricci flow there are points on the surface with infinite curvature. The transition from incomplete metric to complete metric is instantaneous, in the sense that the metric is complete for all \(t > 0\). A good overview is in “Ricci flows with bursts of unbounded curvature” by Giesen and Topping, arXiv:1302.5686.
Now there are only two cases left. Noncompact Riemann surfaces that are not hyperbolic are either isomorphic to \(\mathbb{C}\) or isomorphic to \(\mathbb{C}^* = \mathbb{C}-\{0\}\). The first case is considered by Li Ma in “Convergence of Ricci flow on \(R^2\) to the plane”, and it is shown that additional assumptions are needed in order to have some convergence to the Euclidean metric. The case \(\mathbb{C}^*\) seems to be the case for which the least is known, but I might have missed things.
