Knot groups are the groups that appear as fundamental groups of R3−K where K⊆R3 is a knot. At the moment, I am most interested in the case where K is the trefoil knot, because in this case the knot group is isomorphic to the braid group on 3 strands. I want to show some pictures of the Cayley graphs for knot groups, and share the Python code that I used to generate them.
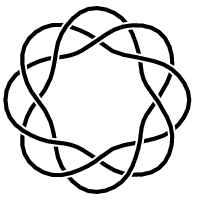
Here is a picture of the trefoil knot:

Sometimes it makes sense to distinguish this trefoil knot from its mirror image below:

But up to homeomorphism R3−K is independent of whether you take K to be the left-handed or right-handed version of the trefoil knot. So the knot group π1(R3−K) is also independent of this choice, which is why for our purposes the two trefoil knots are the same.
Torus knots
The algorithm for drawing the Cayley graphs works not only for the trefoil knot, but more generally for torus knots.
If n and m are two coprime natural numbers, then the (n,m)-torus knot is the knot that you get by winding a string around a donut, in such a way that you go through the donut hole n times, while at the same time circling around the hole m times. In symbols, you take the map S1→S1×S1, z↦(zn,zm) and then you embed S1×S1 into R3 in the standard way.
For example, the trefoil knot is the (3,2)-torus knot.
If K is an (n,m)-torus knot, then you can show that the knot group π1(R3−K) has two generators, say x and y, with one relation between the generators: xn=ym. This is shown in Hatcher’s Algebraic Topology, Example 1.24. For the special case of the trefoil knot, you can look at the references here.
Cayley graph for the trefoil knot group
Now some pictures of the Cayley graphs of knot groups.
First we look at the trefoil knot group:

The elements of the group that are pictured are the ones that can be written as a word with the letters x and y and of length at most 5. The elements for which you need x−1 or y−1 are ignored.
Each time you multiply by x or y, you follow one of the “spirals” upstairs. If you choose x, then you follow an arc of angle 120∘ until you arrive at the next element of the group. If you choose y, then you follow an arc of angle 180∘ to get to the next element.

If my description is not too confusing, you should be able to see the relation x3=y2 in the Cayley graph.
Here is a picture of the same Cayley graph, as seen from above:

Each of the circles corresponds to a spiral staircase that keeps going up, corresponding to a sequence g, gx, gx2, gx3, gx4, … or a sequence g, gy, gy2, gy3, gy4, … in the Cayley graph.
Cayley graphs for torus knot groups
Seen from above, the Cayley graphs of the (n,m)-torus knot group always look a bit similar. Here are the Cayley graphs for (n,m)=(4,3) and (n,m)=(7,5), from above.
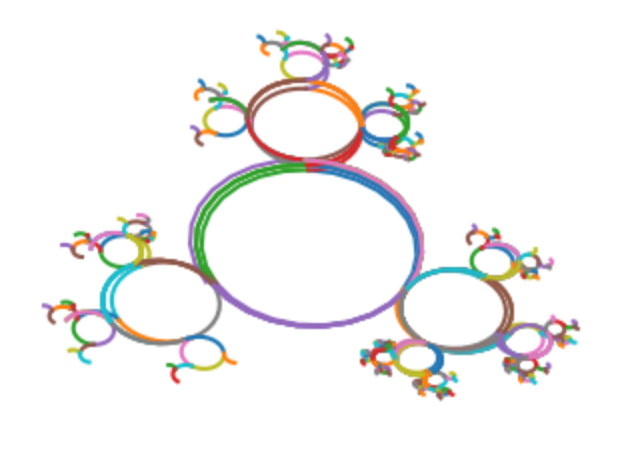
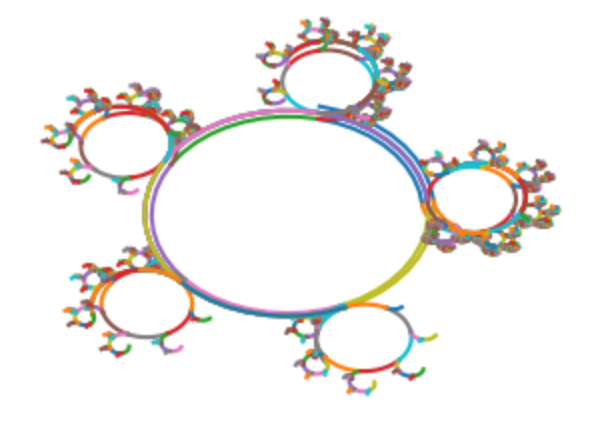
The Cayley graphs seem to get more complicated as n and m get larger. For example, here is the Cayley graph (n,m)=(7,5), seen from the front.

References
The idea to construct the Cayley graphs in this way is from Hatcher’s Algebraic Topology, Example 1.35. But my original motivation to try to draw the Cayley graph comes from this StackExchange question. There the “OP” draws the Cayley graph of the 3-strand braid group, in a very clear and beautiful way. The question is whether the drawing is correct (unanswered at the moment). The 3-strand braid group ⟨a,b:aba=bab⟩ is isomorphic to the trefoil knot group via the substitutions x=ab and y=aba.
Python code
You can view, edit and run the Python code here.
If this does not work, you can also download the code here, and run it using your own installation of Jupyter notebook with Python 3.
To get the Cayley graph for the (n,m)-torus knot group, set N_x to n and N_y to m, or vice versa. Aside from N_x and N_y the most important parameter is depth. The number of arrows that are drawn is equal to 2depth+1. With my laptop and my patience, depth=10 is the maximum.
